Algebraic Topology I

Course Overview

The course will give an introduction to algebraic topology with a focus on homotopy theory. We will consider the classifying space of a small category and develop the homotopy theoretical methods used to study its homotopy type. Later in the course, we will define and study algebraic K-theory.

Object of the course

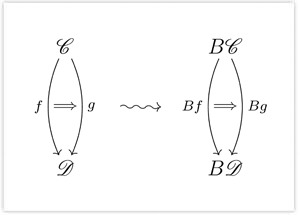
To every category 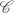, we associate a topological space 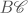. The space 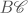is called the classifying space of 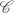. A functor 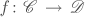gives rise to a continuous map 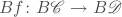. Moreover, a natural transformation from the functor 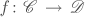to the functor 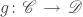gives rise to a homotopy 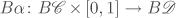from the map 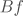to the map 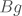. In short, the classifying space construction gives rise to a 2-functor from the 2-category of categories to the 2-category of topological spaces. In this way, properties of categories are reflected in the homotopy type of their classifying spaces.

The classifying space is constructed by gluing together simplices

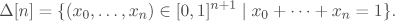
The general recipe for constructing a topological space by gluing together simplices is called a simplicial set. The resulting topological space is called the geometric realization of the simplicial set. The first part of the course will focus on simplicial sets and their geometric realization along with the basic category theoretical notions of limits and colimits and adjoints functors which are needed to develop this theory.

The next part of the course focuses on homotopy theory. We introduce homotopy groups and define a continuous map between topological spaces to be a weak equivalence if it induces an isomorphism of the associated homotopy groups. The homotopy category of topological spaces to be the category obtained from the category of topological spaces and continuous maps by formally introducing an inverse map for every weak equivalence. The main techniques for studying the homotopy category are centered around two classes of maps called the fibrations and the cofibrations. The category of topological spaces together with the three classes of maps given by the weak equivalences, the fibrations, and the cofibrations form a model category. In homotopy theory, theorems live in the homotopy category, but their proofs live in the model category.

The final part of the course uses the techniques we have developed to define algebraic K-theory. We prove the so-called additivity theorem from which many of the basic properties of algebraic K-theory are readily derived.

Keywords

Homotopy theory, model categories, algebraic K-theory.

Required knowledge

An introductory course in algebraic topology including the fundamental group and covering spaces.

Texts

The course lecture notes. The following texts are also useful:

• Mark Hovey, Model Categories, Mathematical Surveys and Monographs, vol. 63, American Mathematical Society.
• Daniel G. Quillen, Homotopical Algebra, Lecture Notes in Mathematics, vol. 43, Springer-Verlag, New York.
• Friedhelm Waldhausen, Algebraic K-theory of spaces, Lecture Notes in Mathematics, vol. 1126, Springer-Verlag, New York.

Related Recources

Mark Hovey, Model Categories, Mathematical Surveys and Monographs, vol. 63, American Mathematical Society.

Daniel G. Quillen, Homotopical Algebra, Lecture Notes in Mathematics, vol. 43, Springer-Verlag, New York.

Friedhelm Waldhausen, Algebraic K-theory of spaces, Lecture Notes in Mathematics, vol. 1126, Springer-Verlag, New York.

Assignments

• Problem set 1.
• Problem set 2.

Course Schedule

Session	Contents
1	The classifying space of a category.
2	The geometric realization of a simplicial set.
3	Limits and colimit; filtered colimits and finite limits commute.
4	Adjoint functors, limits and colimits.
5	Characterizing the geometric realization by maps from it.
6	Geometric realization preserves finite products; k-spaces.
7	Homotopy groups; mapping fiber; long-exact sequence.
8	The classifying space of a finite group. (I recommend to skip this lecture.)
9	Weak equivalences, Serre fibrations, Serre cofibrations; Quillen model categories.
10	The homotopy category; Quillen functors.
11	Reedy model structure on the category of simplicial spaces; geometric realization is a left Quillen functor.
12	Bi-simplicial sets and their geometric realization; geometric realization and weak equivalences; Quillen's Theorem A and B.
13	Algebraic K-theory.
14	The additivity theorem.
15	Hochschild homology of a ringoid: An introduction.

Lecture Handouts

Session #1

• The classifying space of a category.

Session #2

• The geometric realization of a simplicial set.

Session #3

• Limits and colimit; filtered colimits and finite limits commute.

Session #4

• Adjoint functors, limits and colimits.

Session #5

• Characterizing the geometric realization by maps from it.

Session #6

• Geometric realization preserves finite products; k-spaces.

Session #7

• Homotopy groups; mapping fiber; long-exact sequence.

Session #8

• The classifying space of a finite group.

Session #9

• Weak equivalences, Serre fibrations, Serre cofibrations; Quillen model categories.

Session #10

• The homotopy category; Quillen functors.

Session #11

• Reedy model structure on the category of simplicial spaces; geometric realization is a left Quillen functor.

Session #12

• Bi-simplicial sets and their geometric realization; geometric realization and weak equivalences; Quillen's m A and B.

Session #13

• Algebraic K-theory.

Session #14

• The additivity theorem.

Session #15

• Hochschild homology of a ringoid: An introduction.

Grading

Occasional exercises reviewed by the teacher.

---